横截相交

两个 子流形 和 在环境空间 中横截相交，如果对于所有 ，

其中加法在 中进行，并且 表示 的 切映射。如果两个子流形不 相交，则它们自动横截。例如， 中的两条曲线仅当它们根本不 相交 时才横截。当 和 横截相遇时， 是预期维度为 的光滑 子流形。

在某种意义上，两个子流形“应该”横截 相交，并且根据 Sard 定理，任何交集都可以扰动为横截的。同调中的交集只有在交集可以变为横截时才有意义。

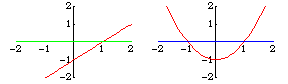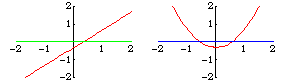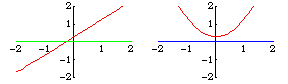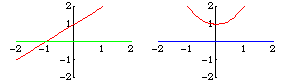
横截性是扰动后交集保持稳定的充分条件。例如，直线 和 横截 相交，扰动后的直线 也是如此，它们仅在一个点 相交。然而， 与 不是横截 相交。它在一个点 相交，而 则在零个或两个点 相交，具体取决于 是正数还是负数。

当 时，横截相交是 孤立点。如果这三个空间具有 向量空间定向，则横截条件意味着可以为交集分配符号。如果 是 的定向基，并且 是 的定向基，则如果 在 中定向，则交集为 ，否则为 。

更一般地，如果每当 时，都有 ，则两个 光滑映射 和 是横截的。