Limaçon Trisectrix

蚌线三等分角线是一种 三等分角线，是 玫瑰线 的一个特例，其 （可能经过平移、旋转和缩放）。 阿基米德以及 Étienne Pascal 在 1630 年研究了它。

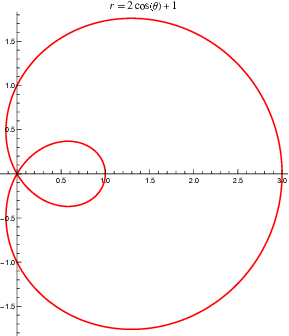
在其最常见的标准形式中，蚌线三等分角线具有 极坐标方程

(1)

（Ferréol）。 它可以表示为 笛卡尔方程

(2)

或

(3)

蚌线三等分角线是相对于其蚌线圆中心而言的 心脏线踏板曲线（Ferréol）。

它具有 弧长

(4)

其中 是 第二类完全椭圆积分。 它的外边界包围的面积为

(5)

其内部环的面积为

(6)

作为 玫瑰线 的一个特例，极坐标方程 由下式给出

(7)

这必须旋转 度，按 2 的因子缩放，向右平移距离 1，并从 到 绘制，以获得标准形式的曲线。