圆柱-圆柱 相交

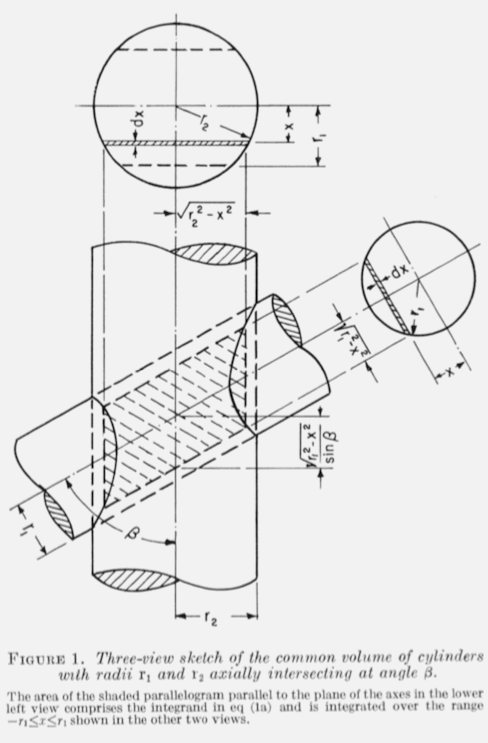
考虑如上图所示的两个圆柱体（Hubbell 1965），其中圆柱体的半径为 和 ，且 ，较大的圆柱体沿 -轴方向，并且两个圆柱体的轴线以角度 相交。那么相交区域的体积由下式给出

			(1)
			(2)
			(3)
			(4)
			(5)

其中

(6)

这里， 和 分别是第一类和第二类完全椭圆积分， 是一个超几何函数，而 是一个二项式系数。

两个（或三个）半径相等的直圆柱以直角相交的交集被称为施泰因梅茨体。