n-流形 和
的连通和
是通过删除
-球
在
的内部,并将由此产生的穿孔流形
通过同胚
相互连接而形成的,因此
需要 在
的内部,且
在
中是双领的,以确保连通和是一个流形。
在拓扑上,如果 和
是道路连通的,那么连通和与
和
上连接被粘合的位置的选择无关。
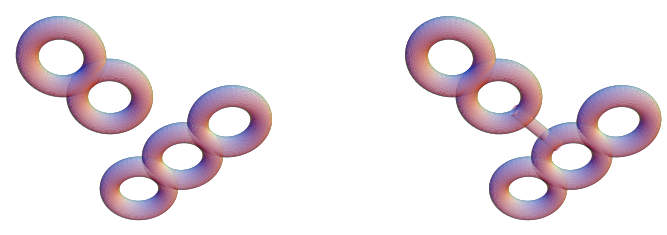
上面的图示显示了两个环面(顶部图)和两对多把环面的连通和。
n-流形 和
的连通和
是通过删除
-球
在
的内部,并将由此产生的穿孔流形
通过同胚
相互连接而形成的,因此
需要 在
的内部,且
在
中是双领的,以确保连通和是一个流形。
在拓扑上,如果 和
是道路连通的,那么连通和与
和
上连接被粘合的位置的选择无关。
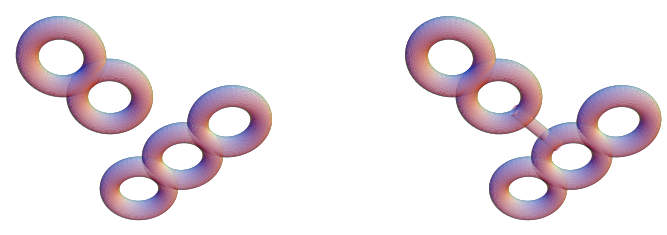
上面的图示显示了两个环面(顶部图)和两对多把环面的连通和。
本条目的部分内容由 Todd Rowland 贡献
Rowland, Todd 和 Weisstein, Eric W. "连通和。" 来自 --一个 资源。 https://mathworld.net.cn/ConnectedSum.html