一个代数曲面,具有仿射方程
 |
(1)
|
其中  是第一类切比雪夫多项式,
是第一类切比雪夫多项式, 是由下式定义的多项式
是由下式定义的多项式
 |
(2)
|
其中矩阵的维度为  。这些表示
。这些表示  中的曲面,其奇点仅为普通二重点。前几个曲面由下式给出
中的曲面,其奇点仅为普通二重点。前几个曲面由下式给出
阶数为  的此类曲面具有
的此类曲面具有
 |
(6)
|
个奇点 (Chmutov 1992),给出序列 0, 1, 3, 14, 28, 57, 93, 154, 216, 321, 425, 576, 732, 949, 1155, ... (OEIS A057870),对于  , 2, .... 对于许多阶数
, 2, .... 对于许多阶数  ,Chmutov 曲面比任何其他已知同 degree 方程具有更多的普通二重点。
,Chmutov 曲面比任何其他已知同 degree 方程具有更多的普通二重点。
基于 Chmutov 的方程,Banchoff (1991) 定义了更简单的一组曲面
 |
(7)
|
其中  是偶数,
是偶数, 再次是第一类切比雪夫多项式。例如,上面所示的曲面阶数为 2、4 和 6,由以下方程给出
再次是第一类切比雪夫多项式。例如,上面所示的曲面阶数为 2、4 和 6,由以下方程给出
另请参阅
Goursat 曲面,
普通二重点,
超椭圆,
Tanglecube
使用 探索
参考文献
Banchoff, T. F. "Computer Graphics Tools for Rendering Algebraic Surfaces and for Geometry of Order." 在 Geometric Analysis and Computer Graphics: Proceedings of a Workshop Held May 23-25, 1988 (编 P. Concus, R. Finn, and D. A. Hoffman). New York: Springer-Verlag, 页 31-37, 1991.Chmutov, S. V. "Examples of Projective Surfaces with Many Singularities." J. Algebraic Geom. 1, 191-196, 1992.Hirzebruch, F. "Singularities of Algebraic Surfaces and Characteristic Numbers." 在 The Lefschetz Centennial Conference, Part I: Proceedings of the Conference on Algebraic Geometry, Algebraic Topology, and Differential Equations, Held in Mexico City, December 10-14, 1984 (编 S. Sundararaman). Providence, RI: Amer. Math. Soc., 页 141-155, 1986.Sloane, N. J. A. 序列 A057870,来自 “整数序列在线大全”。Trott, M. Graphica 1: The World of Mathematica Graphics. The Imaginary Made Real: The Images of Michael Trott. Champaign, IL: Wolfram Media, 页 3 和 82, 1999.Trott, M. The Mathematica GuideBook for Graphics. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
请引用为
Weisstein, Eric W. “Chmutov 曲面。” 来自 Web 资源。 https://mathworld.net.cn/ChmutovSurface.html
主题分类
是第一类切比雪夫多项式,
是由下式定义的多项式

。这些表示
中的曲面,其奇点仅为普通二重点。前几个曲面由下式给出
的此类曲面具有

, 2, .... 对于许多阶数
,Chmutov 曲面比任何其他已知同 degree 方程具有更多的普通二重点。

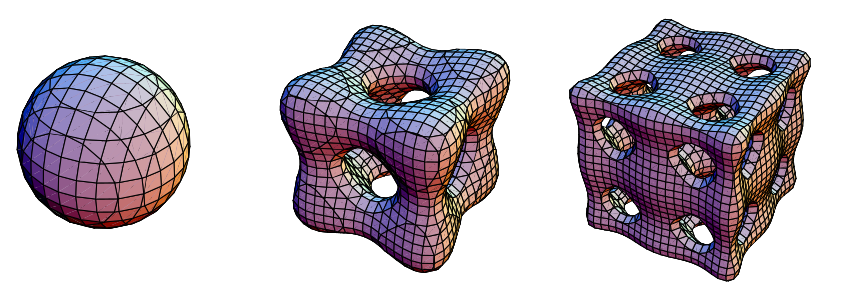
是偶数,
再次是第一类切比雪夫多项式。例如,上面所示的曲面阶数为 2、4 和 6,由以下方程给出