凯西定理

四个圆 、 、 和 与第五个圆或一条直线直线当且仅当相切时，

其中 是圆 圆 和 的公切线的长度 (Johnson 1929, pp. 121-122)。以下情况是可能的：

1. 如果所有的 s 都是外公切线，那么 与所有圆都有同向接触，

2. 如果来自一个圆的 s 是内公切线，而其他三个是外公切线，那么这个圆与 的接触方式与其他三个不同，

3. 如果给定的圆可以成对配对，使得每对圆的公切线是外公切线，而其他四个是内公切线，那么每对的成员与 具有同向接触

(Johnson 1929, p. 125)。

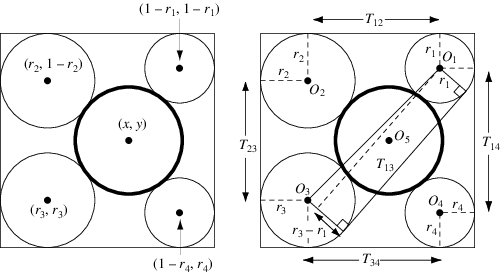
上面显示的凯西定理的特殊情况是在群马县 1874 年的算额问题中给出的。在这种形式中，一个圆绘制在一个正方形内部，然后在其周围绘制四个圆，每个圆都与正方形的两条边相切。对于边长为 且左下角位于 的正方形，其中包含一个半径为 中心为 的中心圆，可以通过求解以下方程找到四个圆的半径和位置：

定理的四个 对于该图立即给出为

剩余的 和 可以如图右所示找到。设 是从 到 的距离，则

因此

由于四个圆都与 外切，因此要使用的凯西定理的相关形式具有符号 ，因此我们有以下等式：

(Rothman 1998)。然后求解 得到关系式

Durell (1928) 将以下定理称为凯西定理：如果 是半径为 和 的两个圆的公切线长度， 是它们相对于任何点的反演的对应公切线长度，并且 和 是它们反演的半径，那么