 |
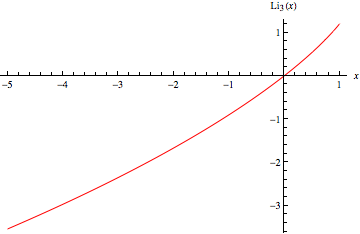
三重对数 , 有时也表示为
, 是 多重对数
在
时的特殊情况。 请注意,三重对数
的符号不幸地与 对数积分
的符号相似。
三重对数在 Wolfram 语言 中实现为PolyLog[3, z].
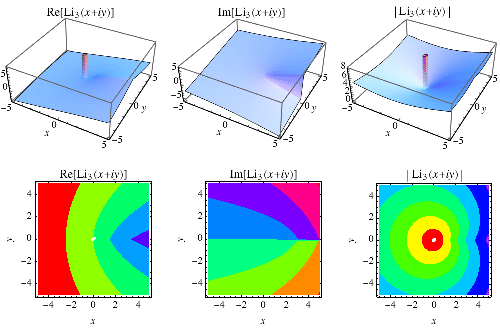 |
上图展示了 在复平面上的图。
三重对数的功能方程包括
 |
(1)
|
的解析值包括
![Li_3(-1)=-3/4zeta(3)
Li_3(0)=0
Li_3(1/2)=1/(24)[-2pi^2ln2+4(ln2)^3+21zeta(3)]
Li_3(1)=zeta(3)
Li_3(phi^(-2))=4/5zeta(3)+2/3(lnphi)^3-2/(15)pi^2lnphi](/images/equations/Trilogarithm/NumberedEquation2.svg) |
(2)
|
Bailey 等人证明了
 |
(3)
|
 |
三重对数 , 有时也表示为
, 是 多重对数
在
时的特殊情况。 请注意,三重对数
的符号不幸地与 对数积分
的符号相似。
三重对数在 Wolfram 语言 中实现为PolyLog[3, z].
 |
上图展示了 在复平面上的图。
三重对数的功能方程包括
 |
(1)
|
的解析值包括
![Li_3(-1)=-3/4zeta(3)
Li_3(0)=0
Li_3(1/2)=1/(24)[-2pi^2ln2+4(ln2)^3+21zeta(3)]
Li_3(1)=zeta(3)
Li_3(phi^(-2))=4/5zeta(3)+2/3(lnphi)^3-2/(15)pi^2lnphi](/images/equations/Trilogarithm/NumberedEquation2.svg) |
(2)
|
Bailey 等人证明了
 |
(3)
|
Weisstein, Eric W. “三重对数。” 来自 Web 资源。 https://mathworld.net.cn/Trilogarithm.html