移动沙发问题

Moser (1966) 提出了以下问题：在单位宽度的二维走廊中，面积最大的平面图形（“沙发”） 能够绕过直角拐角移动。一个面积为 的单位正方形 可以很容易地“绕过”拐角移动，只需沿着走廊推动它直到碰到远处的墙壁，然后沿着垂直的走廊拉动它即可，如上图所示（Rommik 2016）。

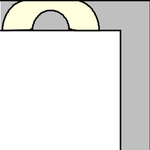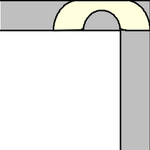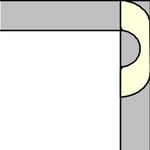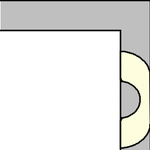
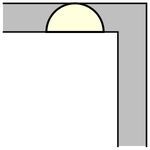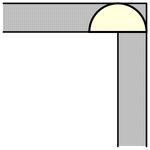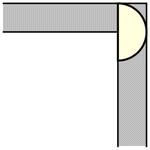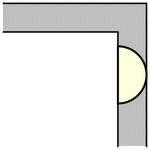
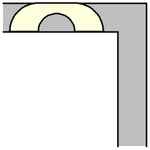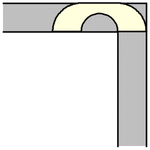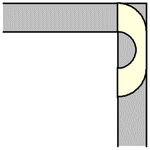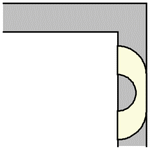
虽然单位正方形可以在不旋转的情况下“绕过”拐角移动，但当允许旋转时，移动更大的形状是可能的。要考虑的最简单的这种形状是半单位圆盘（填充的半圆），其面积为 ，它可以像上图所示那样滑过拐角（Rommik 2016）。

Hammersley（Croft等人1994，Rommik）通过将半圆盘切割成两个四分之一圆盘进一步增加了面积，将它们水平分隔开 的距离，同时填充它们之间的间隙。此外，他从底部移除了一个半径为 的较小半圆盘，从而产生了一个可以称为 Hammersley 沙发 的形状。当 时，其面积最大化，得到面积

（OEIS A086118；Croft等人1994，Rommik）。事实证明，对于任何值 ，包括给出最大面积的半径 ，Hammersley 沙发都可以绕过拐角移动。最大 Hammersley 沙发绕过拐角的过程如上图所示（Romik 2016）。

Gerver (1992) 发现了一种面积为 2.219531...（OEIS A128463；这个数字可以称为 移动沙发常数）的沙发，略大于 Hammersley 最优沙发的面积 2.207416...（OEIS A086118）。这种沙发可以绕过拐角移动，Gerver (1992) 提供的论证表明它要么是最优的，要么接近最优。Gerver 沙发的边界是一个复杂的形状，由 3 条直线段和 15 个曲线段组成，每个曲线段都由解析表达式描述。Gerver 沙发绕过转角的动画如上图所示（Romik 2016）。

假设轨迹和包络线是凸的，Deng (2024) 使用变分法在一组曲线的参数方程上构建了一个积分泛函，通过求解欧拉-拉格朗日微分方程来确定沙发形状。使用数值方法，这给出了一个面积为 2.2195316 的形状，与 Gerver 沙发一致。Baek (2024) 证明了 Gerver 的构造达到了最大面积 2.2195...，其证明不需要计算机辅助，只需使用科学计算器进行数值计算即可。