Hammersley 沙发

在移动沙发问题中，即寻找最大面积 的平面图形（“沙发”），使其能够在一个单位宽度的二维走廊的直角转角处移动，Hammersley（Croft et al. 1994, Rommik）发现了一种形状，其面积大于半圆盘，方法是将半圆盘切割成两个四分之一圆盘，水平分隔一段距离 ，同时填充它们之间的间隙。此外，从底部移除了一个半径为 的较小半圆盘，如上图所示。

所得的“Hammersley 沙发”如上图所示，针对不同的 值，形状从 时的半圆盘变为 时两半在单点相遇的形状。

Hammersley 沙发的面积

(1)

和周长

(2)

正如预期的那样，当 时，面积和周长会减小到半圆盘 和 的值。上面显示了 作为 从 到 的函数图。

当 最大化时，，得到面积

(3)

（OEIS A086118； Croft et al. 1994, Rommik）。

最大 Hammersley 沙发如上图所示。

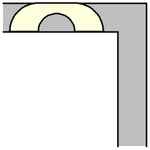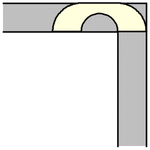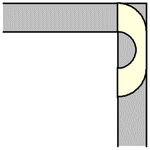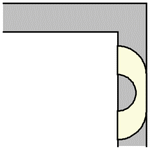
事实证明，对于任何值 ，包括给出最大面积的半径 ，Hammersley 沙发都可以绕过角落。上面展示了最大 Hammersley 沙发绕过角落的过程 (Romik 2016)。

后来发现了一种稍大的沙发，现在称为Gerver 沙发，并最终被证明是最佳的。