主题
Search

Chen-Gackstatter 曲面

一类源自 Enneper 极小曲面的 完备 可定向 极小曲面，位于 R^3 中。它们以 1982 年发现前两个例子的数学家命名。

Chen-Gackstatter 曲面构成双索引集合 M_(ij)，其中 i>=0 且 j>=1。M_(0,1) 是 Enneper 极小曲面，M_(i1) 是通过在 M_(0,1) 上添加 i 个柄而获得的，使其拓扑亏格等于 i。它有一个卷绕阶数为 3 的 Enneper 端，这意味着，与 Enneper 极小曲面一样，它具有对称的三重形状，并且在远离中心的地方趋于与三重平面重合。

一般来说，M_(ij) 的 总曲率 为 c=-4pi(i+1)j，拓扑亏格为 ij，并且有一个卷绕阶数为 2j+1 的 Enneper 端。此属性将其与其他曲面（如具有两个卷绕阶数为 1 的端的悬链线面）区分开来。

第一个 Chen-Gackstatter 曲面 M_(1,1) 的拓扑亏格为 p=1，总曲率为 -8pi。它的 Enneper-Weierstrass 参数化 由下式给出

g(z)=(AP^'(z))/(P(z))
(1)
f(z)=2P(z),
(2)

其中 P(z) 是参数为

的 Weierstrass 椭圆函数

g_2=60sum^'_(m,n=-infty)^infty1/((m+ni)^4)
(3)
g_3=0,
(4)

其中 i 是虚数单位（且 g_2 结果为实数且为正数），常数 A 由下式给出

A=sqrt((3pi)/(2g_2)).
(5)

López (1992) 证明了 M_(1,1) 是总曲率为 -8pi 的唯一亏格为 1 的可定向完备极小曲面。

在原点附近，M_(11) 可以用以下参数方程近似表示

x=(4A^2)/(3r^3)cos(3theta)
(6)
y=-(4A^2)/(3r^3)sin(3theta)
(7)
z=(2A)/(r^2)cos(2theta),
(8)

其中 r 是一个小的正数常数，且 0<=theta<=2pi。

第二个 Chen-Gackstatter 曲面 M_(2,1) 的拓扑亏格为 p=2，总曲率为 -12pi。它的 Enneper-Weierstrass 参数化 是

g(z)=B(sqrt(z(z^2-a^2)(z^2-b^2)))/(z^2-a^2)
(9)
f(z)=(z^2-a^2)/(sqrt(z(z^2-a^2)(z^2-b^2))),
(10)

其中 a、b 和 B 是正数，使得 a<b 并且，给定定义

F_1=int_0^a(a^2-x^2)/(sqrt(x(a^2-x^2)(b^2-x^2)))dx
(11)
F_2=int_0^a(x(b^2-x^2))/(sqrt(x(a^2-x^2)(b^2-x^2)))dx
(12)
F_3=int_a^b(x^2-a^2)/(sqrt(x(x^2-a^2)(b^2-x^2)))dx
(13)
F_4=int_a^b(x(b^2-x^2))/(sqrt(x(x^2-a^2)(b^2-x^2)))dx,
(14)

成立

F_1=B^2F_2,
(15)

和

F_1F_4=F_2F_3.
(16)

曲面 M_(1j) 和 M_(2j) 分别由 Karcher (1989) 和 Thayer (1995) 分类。Sato (1996) 完成了所有 M_(ij) 的工作，并证明了 M_(ij) 的 Enneper-Weierstrass 参数化由下式给出

g=cw^i
(17)
f=1/g
(18)

其中

w^(i+1)=(zproduct_(1<=k<=j/2)(z^2-a_(2k)^2))/(product_(1<=l<=(j+1)/2)(z^2-a_(2l-1)^2)),
(19)

且 c, a_1,...,a_j 是合适的实数。可以选择它们，使得三元组

((1/g-g)dh,i(1/g+g)dh,2dh)
(20)

不依赖于 w 的值。

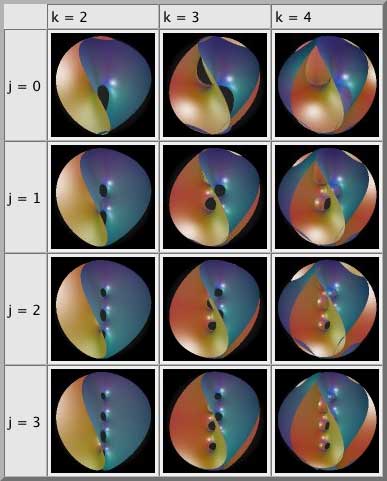
Chen-Gackstatter surfaces

上面的图片（Hoffman 等人）可视化了双索引的作用：M_(ij) 沿其对称轴有 i 个孔，对称轴被一个卷曲的边缘包围，边缘有 j+1 个山峰和山谷。

此条目由 Margherita Barile 贡献

使用 探索

参考文献

Chen, C. C. 和 Gackstatter, F. "Elliptische und hyperelliptische Funktionen und vollständige Minimalflächen vom Enneperschen Typ." Math. Ann. 259, 359-369, 1982.Do Spirito-Santo, N. "Complete Minimal Surfaces in R^3 with Type Enneper End." Ann. Inst. Fourier 44, 525-557, 1994.GRAPE. "Chen-Gackstatter Surface." http://www-sfb256.iam.uni-bonn.de/grape/EXAMPLES/AMANDUS/gackstatter.html.Hoffman, J. T. et al. "The Chen-Gackstatter Thayer Surfaces." http://www.msri.org/publications/sgp/jim/geom/minimal/library/chengack/main.html.Karcher, H. "Construction of Minimal Surfaces." 在 Surveys in Geometry 中. 东京大学, pp. 1-96, 1989.López, F. J. "The Classification of Complete Minimal Surfaces with Total Curvature Greater than -12pi." Trans. Amer. Math. Soc. 334, 49-73, 1992.Sato, K. "Construction of Higher Genus Minimal Surfaces with One End and Finite Total Curvature." Tôhoku Math. J. 48, 229-246, 1996.Thayer, E. C. "Higher-Genus Chen-Gackstatter Surfaces and The Weierstrass Representation for Surfaces of Infinite Genus." Exper. Math. 4, 19-39, 1995.

在 中引用

Chen-Gackstatter 曲面

请引用为

Barile, Margherita. "Chen-Gackstatter 曲面。" 来自 —— 资源，由 Eric W. Weisstein 创建。 https://mathworld.net.cn/Chen-GackstatterSurfaces.html

主题分类