卡塔兰常数 
的简单连分数表示为 [0, 1, 10, 1, 8, 1, 88, 4, 1, 1, ...] (OEIS A014538)。上方显示了以二进制位序列表示的连分数的前 256 项的图。
记录计算总结如下。
| 项 | 日期 | 作者 |
 | 2013年7月20日 | E. Weisstein |
 | 2013年8月7日 | E. Weisstein |
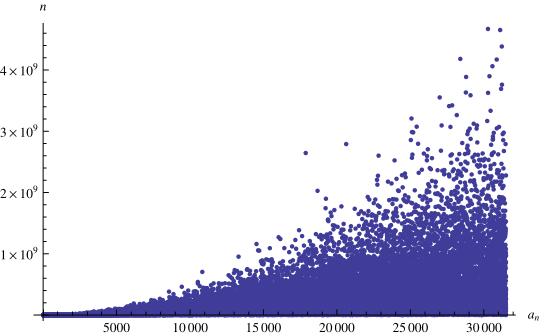
上方图表显示了连分数中 1、2、3、... 首次出现的位置，其中前几个是 1、13、14、7、45、36、10、4、21、2、... (OEIS A196461；如上图所示)。连分数的前 
项中未出现的最小数字是 31516、31591、32600、32806、33410、... (E. Weisstein，2013年8月8日)。
连分数中的累积最大项为 0、1、10、88、322、330、1102、6328、... (OEIS A099789)，它们出现在位置 0、1、2、6、105、284、747、984、2230、5377、... (OEIS A099790)。
设 
的连分数表示为 ![[a_0;a_1,a_2,...]](/images/equations/CatalansConstantContinuedFraction/Inline6.svg)
，并设收敛项的分母表示为 
、
、...、
。那么，上面的图表显示了 
、
、
的连续值，它们似乎收敛于辛钦常数（左图），以及 
，它似乎收敛于列维常数（右图），尽管这些极限都尚未得到严格证明。
的 Engel 展开式由 2、2、2、4、4、5、5、12、13、41、110、... (OEIS A054543) 给出。
