 |  | ![[0.85 0.04; -0.04 0.85][x; y]+[0.00; 1.60]](/images/equations/BarnsleysFern/Inline3.svg) |
(1)
|
 |  | ![[-0.15 0.28; 0.26 0.24][x; y]+[0.00; 0.44]](/images/equations/BarnsleysFern/Inline6.svg) |
(2)
|
 |  | ![[0.20 -0.26; 0.23 0.22][x; y]+[0.00; 1.60]](/images/equations/BarnsleysFern/Inline9.svg) |
(3)
|
 |  | ![[0.00 0.00; 0.00 0.16][x; y]](/images/equations/BarnsleysFern/Inline12.svg) |
(4)
|
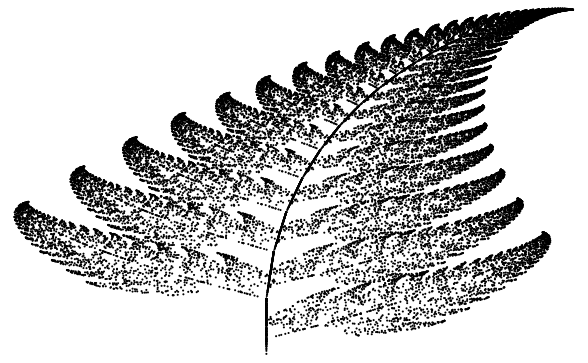
(Barnsley 1993, p. 86; Wagon 1991)。 这些仿射变换是收缩。 蕨类的尖端（类似于黑 spleenwort 品种的蕨类植物）是 
的不动点，最低两个分支的尖端是 
和 
下主尖端的图像 (Wagon 1991)。
Barnsley's Fern
另请参阅
Barnsley's Tree, 动力系统, 分形, 迭代函数系统使用 Wolfram|Alpha 探索
参考文献
Barnsley, M. Fractals Everywhere, 2nd ed. Boston, MA: Academic Press, pp. 86, 90, 102 and Plate 2, 1993.Gleick, J. Chaos: Making a New Science. New York: Penguin Books, p. 238, 1988.Trott, M. Graphica 1: The World of Mathematica Graphics. The Imaginary Made Real: The Images of Michael Trott. Champaign, IL: Wolfram Media, pp. 46, 55, and 87, 1999.Wagon, S. "Biasing the Chaos Game: Barnsley's Fern." §5.3 in Mathematica in Action. New York: W. H. Freeman, pp. 156-163, 1991.在 Wolfram|Alpha 中引用
Barnsley's Fern请引用为
Weisstein, Eric W. "Barnsley's Fern." 来自 MathWorld--Wolfram 网络资源。 https://mathworld.net.cn/BarnsleysFern.html