在组合逻辑最小化中,一种称为卡诺图的工具经常被使用。它类似于真值表,但是不同的变量沿着两个轴表示,并且以这样的方式排列:从一个方格移动到相邻方格时,只有一个输入位发生变化。它也被称为 Veitch 图、K 图或 KV 图。
卡诺图可用于快速消除布尔函数中的冗余操作。最容易阅读的卡诺图是为完全积或“积之和”形式的函数绘制的图,其中后一个名称也暗示了 AND 和 OR 运算符的使用。在这种函数的典型真值表中,输入使用 0 表示假,1 表示真来枚举,并在作为正二进制整数读取时按计数序列排序。下面说明了四个变量的函数的真值表。
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 0 | 1 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 0 | 1 | 1 | 1 | |
| 0 | 1 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | 0 | |
| 0 | 1 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 1 | 0 | 0 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 0 |
对于表中函数值为 1(真)的行,显示了一个称为最小项的逻辑表达式。最小项使用上划线符号表示 NOT。当所有七个最小项累积时,
|
(1)
|
该函数得以实现。这种实现不是最优的,可以使用卡诺图来简化它。
上面显示了该函数的卡诺图。它是真值表的二维布局。每个维度跨越一对相邻的(但不一定是如此的)变量。变量的序列不是计数序列,而是格雷码,因此在每对相邻单元格(在行或列中)之间,只有一个变量改变状态。
在地图上,函数值为 1 的相邻单元格用环分组在一起。每个环代表可以简化的最小项。环内变化的变量可以被消除。使用最上面的表达式作为示例,可以代数地证明其有效性。
|
(2)
| |||
|
(3)
| |||
|
(4)
|
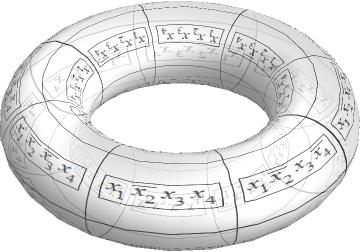
环也可以绘制成环绕行和/或列,因为卡诺图(最多四个变量)实际上是环面的表面。
类似于上面示例的卡诺图也可以类似地为两个(退化)或三个变量绘制。它们可以用于超过四个变量(例如,通过叠加两个四变量图来处理五个变量),但是可视化变得比代数更繁琐。