龙曲线是一种递归的、不相交的曲线,其名称来源于它与某种神话生物的相似之处。
该曲线可以通过将左转表示为 1,右转表示为 0 来构造。一阶曲线因此表示为 1。对于更高阶的曲线,在末尾附加一个 1,然后附加前面数字的字符串,并将其中间数字取反。例如,二阶曲线生成如下:  ,三阶曲线生成如下:
,三阶曲线生成如下:  。
。
继续下去得到 110110011100100... (OEIS A014577),这有时被称为规则的折纸序列,并用  代替 0(Allouche 和 Shallit 2003, p. 155)。上面展示了此序列极限值的递推图。
代替 0(Allouche 和 Shallit 2003, p. 155)。上面展示了此序列极限值的递推图。
将二进制数字序列 1, 110, 1101100, 110110011100100, ... 用八进制表示,得到 1, 6, 154, 66344, ...(OEIS A003460; Gardner 1978, p. 216)。
这个过程等价于绘制一个直角,然后将每个直角替换为另一个更小的直角 (Gardner 1978)。 实际上,龙曲线可以写成Lindenmayer 系统,其初始字符串为"FX",字符串重写规则"X" -> "X+YF+", "Y" -> "-FX-Y",以及角度  。上面展示了 1 到 9 阶的龙曲线,拐角处被圆角化以强调曲线所经过的路径。
。上面展示了 1 到 9 阶的龙曲线,拐角处被圆角化以强调曲线所经过的路径。
另请参阅
杜阿迪兔子分形,
Lindenmayer 系统,
皮亚诺曲线
使用 探索
参考文献
Allouche, J.-P. 和 Mendès France, M. "Automata and Automatic Sequences." 收录于 Beyond Quasicrystals (Ed. F. Axel et al.). Berlin: Springer-Verlag, pp. 293-367, 1994.Allouche, J.-P. 和 Shallit, J. "Example 5.1.6 (The Regular Paperfolding Sequence)." Automatic Sequences: Theory, Applications, Generalizations. Cambridge, England: Cambridge University Press, pp. 155-156, 2003.Bulaevsky, J. "The Dragon Curve or Jurassic Park Fractal." http://ejad.best.vwh.net/java/fractals/jurasic.shtml.Charpentier, M. "L-Systems in PostScript." http://www.cs.unh.edu/~charpov/Programming/L-systems/.Dickau, R. M. "Two-Dimensional L-Systems." http://mathforum.org/advanced/robertd/lsys2d.html.Dixon, R. Mathographics. New York: Dover, pp. 180-181, 1991.Dubrovsky, V. "Nesting Puzzles, Part I: Moving Oriental Towers." Quantum 6, 53-57 (Jan.) 和 49-51 (Feb.), 1996.Dubrovsky, V. "Nesting Puzzles, Part II: Chinese Rings Produce a Chinese Monster." Quantum 6, 61-65 (Mar.) 和 58-59 (Apr.), 1996.Gardner, M. Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 207-209 和 215-220, 1978.Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 48-53, 1991.Mandelbrot, B. B. The Fractal Geometry of Nature. New York: W. H. Freeman, pp. 66-67, 1983.Peitgen, H.-O. 和 Saupe, D. (Eds.). The Science of Fractal Images. New York: Springer-Verlag, p. 284, 1988.Sloane, N. J. A. 序列 A003460/M4300 和 A014577,出自 "The On-Line Encyclopedia of Integer Sequences."Vasilyev, N. 和 Gutenmacher, V. "Dragon Curves." Quantum 6, 5-10, 1995.Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 59, 1991.在 中引用
龙曲线
请引用为
Weisstein, Eric W. "龙曲线。" 来自 Web 资源。 https://mathworld.net.cn/DragonCurve.html
主题分类
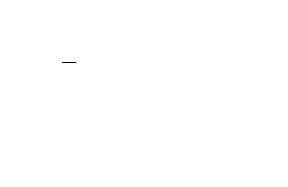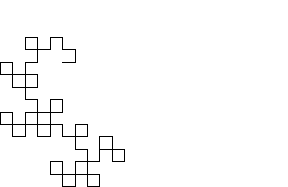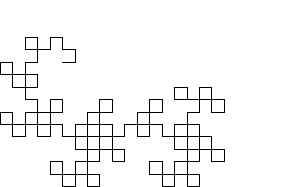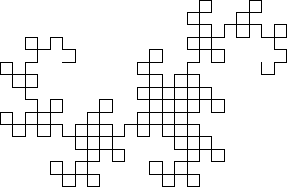
,三阶曲线生成如下:
。

代替 0(Allouche 和 Shallit 2003, p. 155)。上面展示了此序列极限值的递推图。
。上面展示了 1 到 9 阶的龙曲线,拐角处被圆角化以强调曲线所经过的路径。