主题
Search

色根

下载 Mathematica Notebook下载 Wolfram Notebook

色多项式的根被称为色根（Dong et al. 2005, Alikhani and Ghanbari 2024）。色根可能是复数。

Tutte (1970) 证明了 phi+1=phi^2 不可能是任何色多项式的色根，其中，phi 是黄金比例，这一结果被扩展到正整数 n 的 phi^n 情况 (Alikhani and Peng 2009)。

HarveyRoyleGraphs

相反，phi+2 是可能的色根（Harvey 和 Royle 2020；例如，上面描绘的图），这一结果可以扩展到整数 n>=2 的 phi+n 情况（Alikhani 和 Hasni 2012, Alikhani 和 Ghanbar 2024），基于以下结果：如果 alpha 是色根，那么对于任何自然数 n，alpha+n 也是色根。

Sokal (2004) 证明了色根在复平面中是稠密的（Cameron 和 Morgan 2016）。

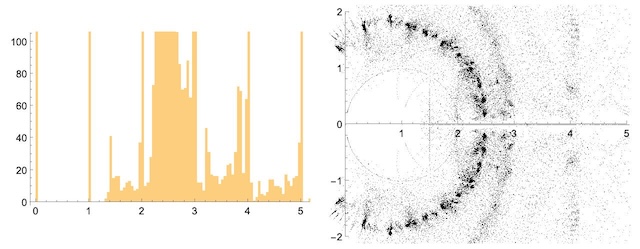
Chromatic roots on the real line and in the complex plane

在其中不可能存在色根的区间被称为无色根区间。上面的图显示了沿实轴的色根直方图以及复平面中 GraphData 中图的色根位置GraphData（后者显示出明显的偏离均匀性）。

另请参阅

色多项式, 无色根区间

使用 Wolfram|Alpha 探索

参考文献

Alikhani, S. and Ghanbari, N. "图论中的黄金比例：综述。" 2024 年 7 月 9 日。 https://arxiv.org/abs/2407.15860.Alikhani, S., Hasni, R. "作为色根和支配根的代数整数。" Int. J. Combin., Article ID 780765, 2012.Alikhani, S. Peng, Y. H. "色零点与黄金比例。" Appl. Anal. Disc. Math. 3, 120-122, 2009.Cameron, P. J. and Morgan, K. "色根的代数性质。" 2016 年 10 月 3 日。 https://arxiv.org/abs/1610.00424.Dong, F. M., Koh, K. M.; and Teo, K. L. 色多项式和图的色性。 新加坡：World Scientific, 2005.Harvey, D. J. and Royle, G. F. "2 处的色根和 Beraha 数 B_(10)。" J. Graph Th. 95, 445-456, 2020.Sokal, A. D. "色根在整个复平面中是稠密的。" Combin. Probab. and Comput. 13, 221-261, 2004.Tutte, W. T. "关于色多项式和黄金比例。" J. Combin. Theory, Ser. B 9, 289-296, 1970.

请引用本文为

Weisstein, Eric W. "色根。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/ChromaticRoot.html

主题分类