在其中对于任何可能的色多项式都不存在色根的区间被称为色根自由区间。一个不能被扩展的色根自由区间被称为极大色根自由区间。
和
是极大根自由区间,如同
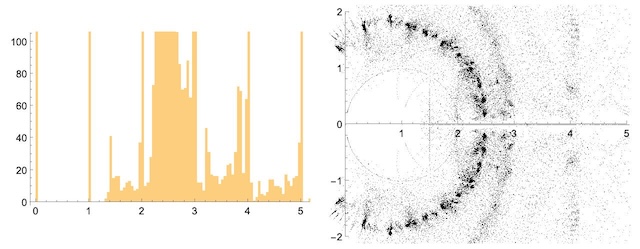
(Jackson 1993, Alikhani and Ghanbari 2024)。此外,色根在复平面中是稠密的 (Sokal 2004, Cameron and Morgan 2016)。上面的图表显示了沿实轴的色根直方图以及在复平面中图的色根位置,这些图来自GraphData(后者显示出明显的偏离均匀性)。
在其中对于任何可能的色多项式都不存在色根的区间被称为色根自由区间。一个不能被扩展的色根自由区间被称为极大色根自由区间。

和
是极大根自由区间,如同
(Jackson 1993, Alikhani and Ghanbari 2024)。此外,色根在复平面中是稠密的 (Sokal 2004, Cameron and Morgan 2016)。上面的图表显示了沿实轴的色根直方图以及在复平面中图的色根位置,这些图来自GraphData(后者显示出明显的偏离均匀性)。
Weisstein, Eric W. "色根自由区间。" 来自 ——Wolfram 网络资源。 https://mathworld.net.cn/ChromaticRoot-FreeInterval.html