如果一个粒子 的半径向量在适当的坐标系中具有形式
,则称该粒子正在进行匀速圆周运动,其中
|
(1)
| |||
|
(2)
|
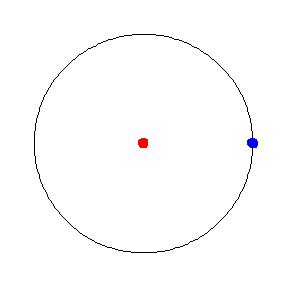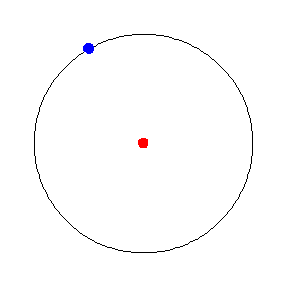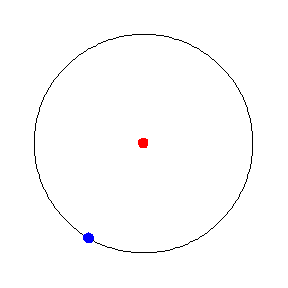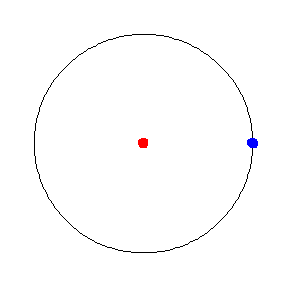
从几何角度来看,匀速圆周运动意味着 在半径为
的
平面中的圆上以恒定速度运动。量
称为
的角速度。
的速度是
|
(3)
|
并且 P 的加速度具有恒定的大小
|
(4)
|
并且指向 所描绘的圆的中心。这称为向心加速度。
忽略其轨道的椭圆率,行星呈现出近似围绕太阳的匀速圆周运动。(尽管由于轨道倾角,不同行星的轨道平面不一定是共面的。)