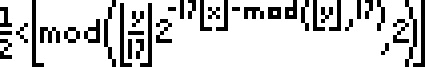
J. Tupper 构思了这个神奇的公式
其中 是地板函数,
是 模 函数,当在
和
范围内绘制图形时,其中
 |
给出了上面所示的自指“图”。
塔珀公式可以推广到其他期望的结果。例如,L. Garron(私人通讯)构建了从 到 29 的推广。
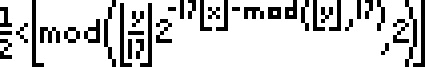
J. Tupper 构思了这个神奇的公式
其中 是地板函数,
是 模 函数,当在
和
范围内绘制图形时,其中
 |
给出了上面所示的自指“图”。
塔珀公式可以推广到其他期望的结果。例如,L. Garron(私人通讯)构建了从 到 29 的推广。
Weisstein, Eric W. "塔珀的自指公式。" 来自 —— 资源。 https://mathworld.net.cn/TuppersSelf-ReferentialFormula.html