协同学坐标

协同学坐标是在其平面上的一组三角形坐标（或它们在空间中的四面体坐标的推广，或更高维度中的类似物）。在平面中，坐标 沿三个轴 、 和 测量，其中 -轴向下定向， 轴和 轴彼此之间以 度角定向，如上图所示（左图）。将 、 和 解释为通过从原点平行位移三对彼此之间以 度角定向的线而获得的等边三角形边上的点，坐标 可以解释为指定给定的等边三角形（右图）。

这些坐标的一个很好的性质是，通过 平行位移获得的三角形的顶点由 、 和 给出（见上图），因此顶点坐标的总和始终为零。当坐标推广到三维和更高维度时，此属性也成立。

协同学坐标还具有以下性质：由 描述的等边三角形的边长恰好是 ，这同样可以推广到更高维度。

协同学坐标为构建规则的圆形和球形堆积提供了一种便捷的方法。例如，左上方所示的圆环可以通过选择所有整数协同学坐标 集来生成，这些坐标的总和为零，并且三个坐标的绝对值之和除以二等于一 (Nelson)。类似地，第二个圆环可以从所有整数坐标集中获得，这些坐标的总和为零，并且三个坐标的绝对值之和除以二等于一。零环、第一环和第二环如右上方所示。

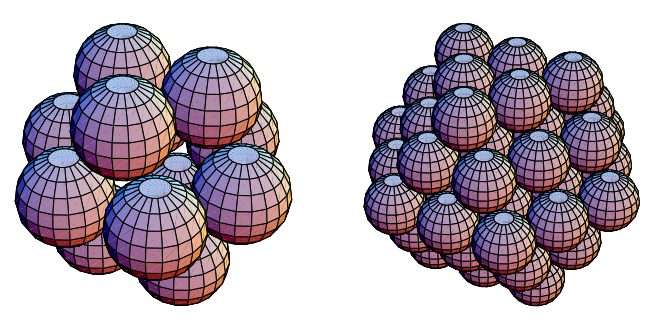
类似的性质在三维中也成立，其中适当的协同学坐标 集在规则球体堆积中给出连续的壳层 (Nelson)，如上图所示。