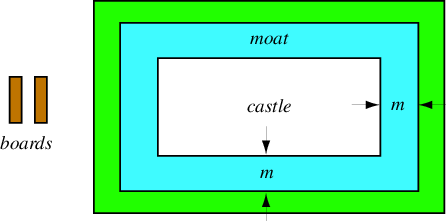
护城河问题有两个版本，一个是几何版本，一个是代数版本。几何护城河问题询问，如果 Rapunzel 只有两块单位长度的木板（且没有钉子或其他方式将它们连接在一起），她可以跨越的最宽的护城河宽度是多少才能逃脱。更一般地，使用 
块木板可以跨越的最宽的护城河宽度是多少？ Matthew Cook 推测，这个问题的渐近解是 
(Cook 1997)。
代数护城河问题询问是否有可能在 实数轴 上仅使用有界长度的步长和素数上的步长走到无穷远。答案是否定的 (Gethner et al. 1998)。然而，高斯护城河问题询问是否有可能在 高斯整数 中使用 高斯素数 作为垫脚石并采取有界长度的步长走到无穷远，这个问题尚未解决。Gethner et al. (1998) 表明，宽度为 
的护城河是存在的。
使用 Wolfram|Alpha 探索
参考文献
Cook, M. "护城河问题更新。" 电子邮件交流，1997年。 http://www.mathcad.com/library/LibraryContent/puzzles/soln26/8b/update.html。Finch, S. "护城河跨越优化问题。" http://www.mathcad.com/library/LibraryContent/puzzles/soln26/soln26.html。Gethner, E. 和 Stark, H. M. "周期性高斯护城河。" 实验数学 6, 251-254, 1997.Gethner, E.; Wagon, S.; 和 Wick, B. "在高斯素数中漫步。" 美国数学月刊 105, 327-337, 1998.Guy, R. K. 数论中未解决的问题，第二版。 纽约：施普林格出版社, 1994.Haugland, J. K. "复素数上的漫步。" [挪威语。] Normat 43, 168-170, 1995.Jordan, J. H. 和 Rabung, J. R. "关于高斯素数的 Paul Erdős 猜想。" 数学计算 24, 221-223, 1970.Montgomery, H. 解析数论与调和分析界面上的十讲。 普罗维登斯，罗德岛州：美国数学学会, 1994.Vardi, I. "素数渗流。" 实验数学 7, 275-289, 1998.Wagon, S. Mathematica 行动，第二版。 纽约：施普林格出版社, 1999.在 Wolfram|Alpha 中被引用
护城河问题
请引用本文为
Weisstein, Eric W. "护城河问题。" 来自 MathWorld--一个 Wolfram Web 资源。 https://mathworld.net.cn/Moat-CrossingProblem.html
主题分类
