椭圆对数是如下形式积分的推广的形状
对于 实数,它可以表示为对数和反三角函数,到
对于 和
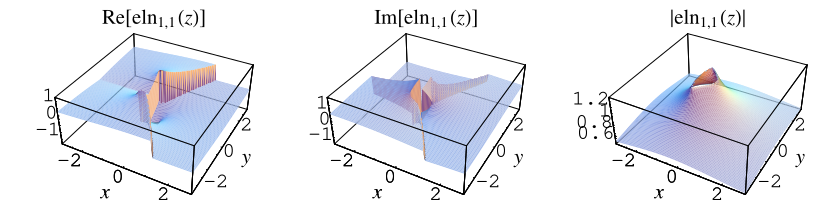
实数。这个积分可以解析地完成,但是具有复杂的形状,涉及到具有复参数的第一类不完全椭圆积分。上面的图显示了特殊情况
。
椭圆对数在 Wolfram 语言 中实现为EllipticLog[x, y
,
a, b
], 其中
是一个不幸且多余的参数,必须设置为
或
,并将上述积分乘以一个因子
。
椭圆对数的逆是椭圆指数函数。

椭圆对数是如下形式积分的推广的形状
对于 实数,它可以表示为对数和反三角函数,到
对于 和
实数。这个积分可以解析地完成,但是具有复杂的形状,涉及到具有复参数的第一类不完全椭圆积分。上面的图显示了特殊情况
。
椭圆对数在 Wolfram 语言 中实现为EllipticLog[x, y
,
a, b
], 其中
是一个不幸且多余的参数,必须设置为
或
,并将上述积分乘以一个因子
。
椭圆对数的逆是椭圆指数函数。
Weisstein, Eric W. "椭圆对数。" 来自 Web 资源。 https://mathworld.net.cn/EllipticLogarithm.html