主题
Search

清洁瓷砖问题

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本

清洁瓷砖是一个由布丰 (Buffon) (1777 年) 研究的游戏，玩家在规则铺砌的地板上投掷硬币，并投注硬币将部分覆盖的不同瓷砖的数量。布丰研究了三角网格、正方网格、六边形网格和由菱形组成的网格上的概率。假设瓷砖的边长 l 大于硬币直径 d。那么，在正方网格上，硬币可能以某种方式落下，使得它部分覆盖 1、2、3 或 4 块瓷砖。在三角网格上，它可以落在 1、2、3、4 或 6 块瓷砖上。在六边形网格上，它可以落在 1、2 或 3 块瓷砖上。

这个游戏的特殊情况给出了 布丰-拉普拉斯针问题（对于正方网格）和 布丰针问题（对于无限等距平行线）。

CleanTileSquare1
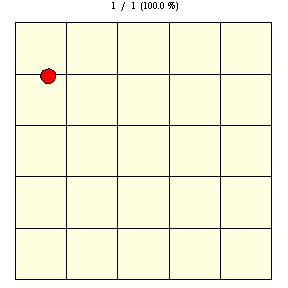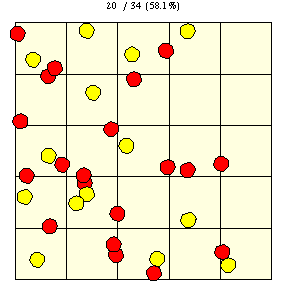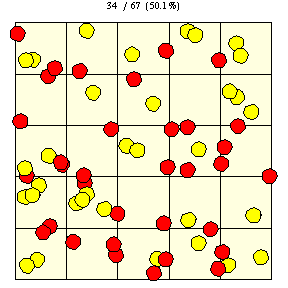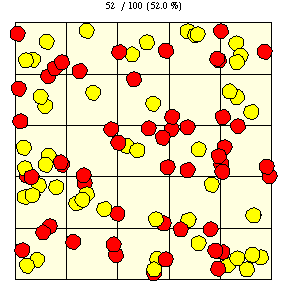
Clean tile on a square grid

如上图所示，在瓷砖边长为 l 的正方网格上，直径为 d 的硬币完全落在单块瓷砖上的概率（图中黄色圆盘所示）由下式给出

P_1=((l-d)^2)/(l^2)=(1-d/l)^2,
(1)

因为通过从边长为 l 的正方形内缩硬币半径 d/2 而得到的正方形边长的缩短量由下式给出

Deltal=2(1/2d)=d.
(2)

它落在两块或更多瓷砖上的概率（红色圆盘所示）仅仅是

P_(>=2)=1-P_1=1-(1-d/l)^2.
(3)

为了使两个玩家分别投注 (1) 单块瓷砖或 (2) 两块或更多瓷砖的游戏公平，这些量必须相等，由此得出

d=1/2(2-sqrt(2))l=0.29289...l.
(4)
CleanTileSquare2

落在恰好两块瓷砖上的概率是上图中阴影区域与瓷砖大小的比率，即

P_2=4d/(2l)(1-d/l)
(5)
=2(1-d/l)d/l.
(6)
CleanTileSquare3

在正方网格上，硬币落在恰好三块瓷砖上的概率是上图中所示区域覆盖的瓷砖部分的比例，

P_3=(d^2-pi(1/2d)^2)/(l^2)=(1-1/4pi)(d^2)/(l^2).
(7)
CleanTileSquare4

类似地，硬币落在四块瓷砖上的概率是上图中所示的圆盘覆盖的瓷砖部分的比例，

P_4=(pi(1/2d)^2)/(l^2)=1/4pi(d^2)/(l^2).
(8)
CleanTileTriangle
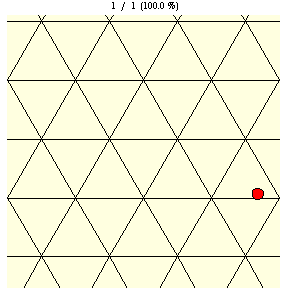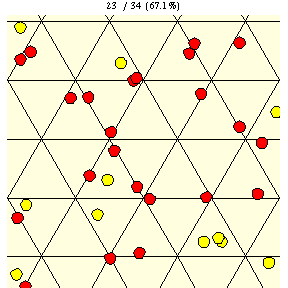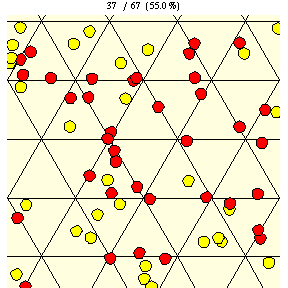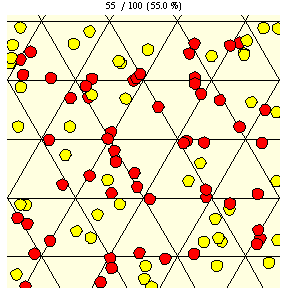
Clean tile on a triangular grid

如上图所示，在瓷砖边长为 l 的三角网格上，直径为 d 的硬币完全落在单块瓷砖上的概率由下式给出

P_1=((l-sqrt(3)d)^2)/(l^2)=(1-sqrt(3)d/l)^2,
(9)

因为通过从边长为 l 的等边三角形内缩硬币半径 d/2 而得到的等边三角形边长的缩短量是

Deltal=2(1/2dcot30 degrees)=sqrt(3)d.
(10)

它落在两块或更多瓷砖上的概率仅仅是

P_(>=2)=1-P_1=1-(1-sqrt(3)d/l)^2.
(11)

为了使两个玩家分别投注 (1) 单块瓷砖或 (2) 两块或更多瓷砖的游戏公平，这些量必须相等，由此得出

d=1/6(2sqrt(3)-sqrt(6))l=0.16910...l.
(12)
CleanTileHexagon

如上图所示，在瓷砖边长为 l 的六边形网格上，直径为 d 的硬币完全落在单块瓷砖上的概率由下式给出

P_1=((l-1/3sqrt(3)d)^2)/(l^2)=(1-1/3sqrt(3)d/l)^2,
(13)

因为通过从边长为 l 的正六边形内缩硬币半径 d/2 而得到的正六边形边长的缩短量是

Deltal=2(1/2d)sec30 degrees=1/3sqrt(3)d.
(14)

它落在两块或更多瓷砖上的概率仅仅是

P_(>=2)=1-P_1=1-(1-1/3sqrt(3)d/l)^2.
(15)

为了使两个玩家分别投注 (1) 单块瓷砖或 (2) 两块或更多瓷砖的游戏公平，这些量必须相等，由此得出

d=1/2(2sqrt(3)-sqrt(6))l=0.50730...l.
(16)
CleanTileRhombus

在由开角为 theta 的菱形组成的四边形平铺中，从边长为 l 的菱形内缩得到

Deltal_1=1/2dcottheta
(17)
Deltal_2=1/2dtantheta,
(18)

因此

Deltal=Deltal_1+Deltal_2=1/2d(cottheta+tantheta)=1/2dcscthetasectheta.
(19)

因此，硬币落在单块瓷砖上的概率是

P_1=((l-1/2dcscthetasectheta)^2)/(l^2)
(20)
=(1-d/(2l)cscthetasectheta)^2.
(21)

它落在两块或更多瓷砖上的概率仅仅是

P_(>=2)=1-P_1=1-(1-d/(2l)cscthetasectheta)^2.
(22)

为了使两个玩家分别投注 (1) 单块瓷砖或 (2) 两块或更多瓷砖的游戏公平，这些量必须相等，由此得出

d=(2-sqrt(2))lcosthetasintheta.
(23)

正如预期的那样，当 theta=pi/4 时，这简化为正方形的情况。

另请参阅

布丰-拉普拉斯针问题, 布丰针问题

使用 Wolfram|Alpha 探索

参考文献

Buffon, G. "Essai d'arithmétique morale." Histoire naturelle, générale er particulière, Supplément 4, 46-123, 1777.Mathai, A. M. "清洁瓷砖问题 (The Clean Tile Problem)." §1.1.1 in 几何概率导论：分布方面及其应用 (An Introduction to Geometrical Probability: Distributional Aspects with Applications). Taylor & Francis: pp. 2-5, 1999.Solomon, H. 几何概率 (Geometric Probability). 美国费城：SIAM, 1978.

在 Wolfram|Alpha 中引用

清洁瓷砖问题

请引用为

Weisstein, Eric W. "清洁瓷砖问题 (Clean Tile Problem)." 来自 MathWorld--Wolfram 网络资源。 https://mathworld.net.cn/CleanTileProblem.html

学科分类