参见
Barnsley 蕨叶,
谢尔宾斯基筛
使用 Wolfram|Alpha 探索
参考文献
Borwein, J. 和 Bailey, D. “帕斯卡三角形。” §2.1 in Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 47-48, 2003.Barnsley, M. F. 和 Rising, H. Fractals Everywhere, 2nd ed. Boston, MA: Academic Press, 1993.Bogomolny, A. “谢尔宾斯基垫片与混沌游戏。” http://www.cut-the-knot.org/Curriculum/Geometry/SierpinskiChaosGame.shtml.Dickau, R. M. “混沌游戏。” http://mathforum.org/advanced/robertd/chaos_game.html.Jeffrey, H. J. “遗传序列的混沌游戏表示。” Nucleic Acids Res. 18, 2163-2170, 1990.Jeffrey, H. J. “序列的混沌游戏可视化。” Comput. & Graphics 16, 25-33, 1992. Reprinted in Chaos and Fractals, A Computer Graphical Journey: Ten Year Compilation of Advanced Research (Ed. C. A. Pickover). Amsterdam, Netherlands: Elsevier, pp. 5-13, 1998.Peitgen, H.-O.; Jürgens, H.; 和 Saupe, D. Fractals for the Classroom, Part 1: Introduction to Fractals and Chaos. New York: Springer-Verlag, pp. 41-43, 1992.Pickover, C. A. (编.). Fractal Horizons: The Future Use of Fractals. New York: St. Martin's Press, pp. 27, 57-59, and 169-171, 1996.Wagon, S. Mathematica in Action, 2nd ed. New York: Springer-Verlag, pp. 226-239, 1999.在 Wolfram|Alpha 上被引用
混沌游戏
请这样引用本文
Weisstein, Eric W. “混沌游戏。” 来自 MathWorld--Wolfram 网络资源。 https://mathworld.net.cn/ChaosGame.html
主题分类
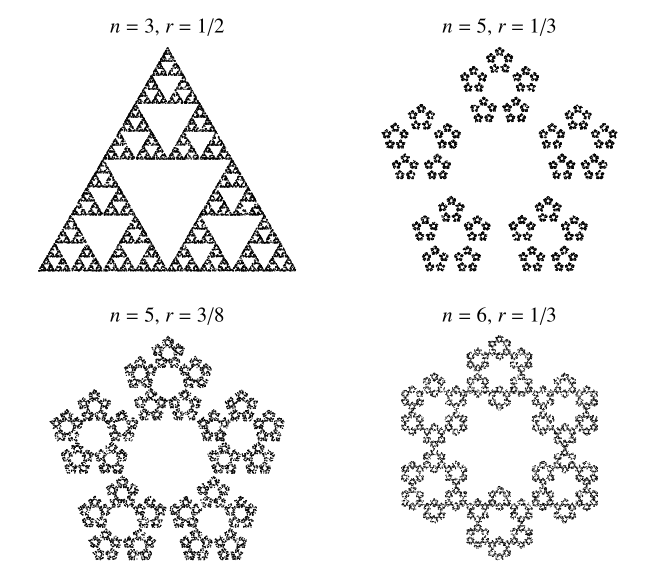
边形内随机选择一个点。然后绘制下一个点，该点与随机选择的多边形顶点之间的距离为 
分之一。继续这个过程（在丢弃最初的几个点之后）。这个“混沌游戏”的结果有时是，但并非总是，一个分形。上面显示了针对几个 
值的混沌游戏结果。
个点，且 
时的混沌游戏。案例 
给出了正方形的内部，所有点被访问的概率均等。
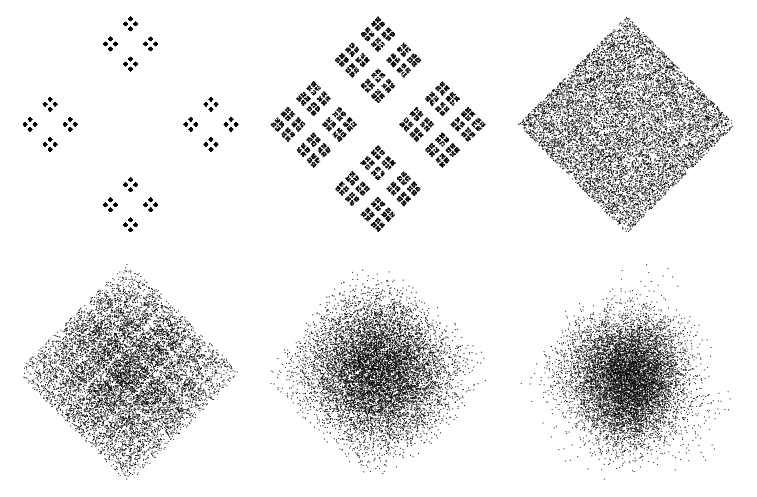
个点，且 
、0.4、0.5、0.6、0.75 和 0.9 时的混沌游戏。