两个轨迹的模式

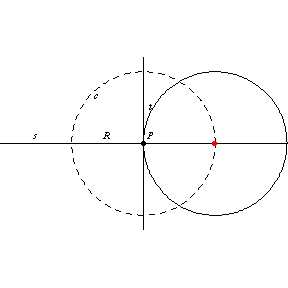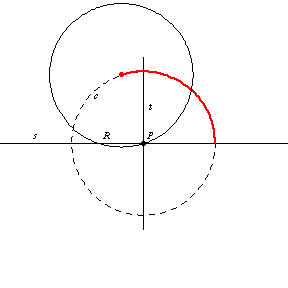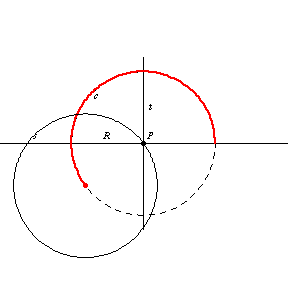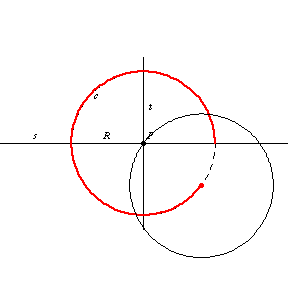
根据 G. Pólya 的说法，这是一种通过相交寻找几何对象的方法。

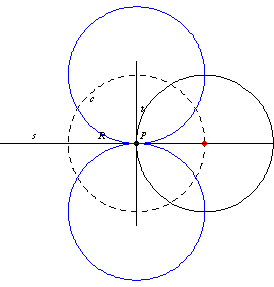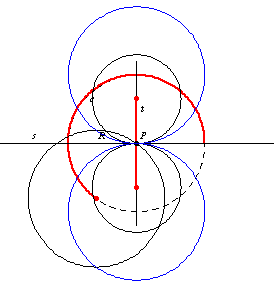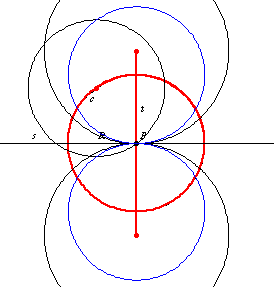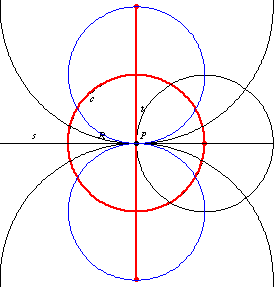
1. 例如，所有与直线 在给定点 相切的圆的圆心都位于通过 且垂直于 的直线 上。

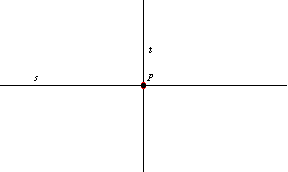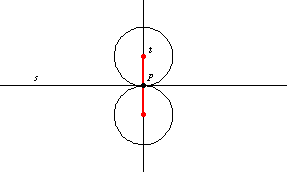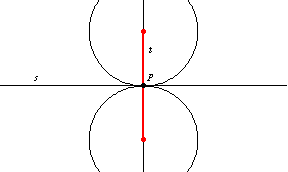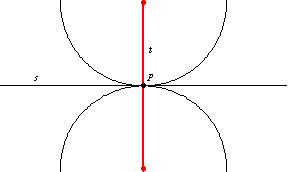
2. 此外，以 为圆心，半径为 的圆 是所有半径为 且经过 的圆的圆心轨迹。

和 的交点由两个点 和 组成，这两个点是半径为 且在 点与 相切的两个圆的圆心。

许多用直尺和圆规进行的构造都基于这种方法，例如，通过垂直平分线定理构造给定圆的圆心。