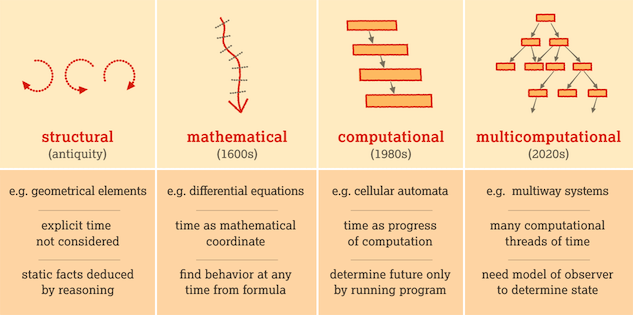
多计算范式是计算范式向多个计算时间线程的推广。在普通的计算范式中，时间有效地以线性方式进行，对应于从前一个状态连续计算系统的下一个状态。相比之下，在多计算范式中，通过计算的每个可能路径都通过不同的交织的时间线程进行。
换句话说，数学范式将时间视为一个数学变量，其值可以任意选择，计算范式将时间视为计算进度的反映，而多计算范式将时间视为多线程，从而反映多个计算线程的交织进展。如上示意图所示，多计算范式可以被视为进行理论科学的新的第四范式，取代了结构范式、数学范式和计算范式（Wolfram 2021a）。
多计算和多计算范式是 Wolfram 物理项目（Wolfram 2021a）的核心思想之一。
参见
计算范式,
数学范式,
多计算不可约性,
多路系统
使用 Wolfram|Alpha 探索
参考文献
Wolfram, S. "Multicomputation: A Fourth Paradigm for Theoretical Science." 2021 年 9 月 9 日. https://writings.stephenwolfram.com/2021/09/multicomputation-a-fourth-paradigm-for-theoretical-science/。Wolfram, S. "Multicomputation with Numbers: The Case of Simple Multiway Systems." 2021 年 10 月 7 日. https://www.wolframinstitute.org/bulletins/2021/10/multicomputation-with-numbers-the-case-of-simple-multiway-systems/。Wolfram, S. "Games and Puzzles as Multicomputational Systems." 2022 年 6 月 8 日. https://writings.stephenwolfram.com/2022/06/games-and-puzzles-as-multicomputational-systems/。Wolfram, S. "Expression Evaluation and Fundamental Physics." 2023 年 9 月 29 日. https://writings.stephenwolfram.com/2023/09/expression-evaluation-and-fundamental-physics/。Wolfram, S. "Contents Aggregation and Tiling as Multicomputational Processes." 2023 年 11 月 3 日. https://writings.stephenwolfram.com/2023/11/aggregation-and-tiling-as-multicomputational-processes/。Wolfram, S. "The Wolfram Physics Project." https://www.wolframphysics.org。
引用为
Weisstein, Eric W. "多计算范式。" 来自 MathWorld--Wolfram Web 资源。 https://mathworld.net.cn/MulticomputationalParadigm.html
主题分类
