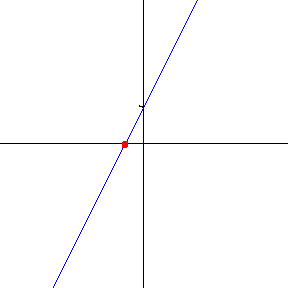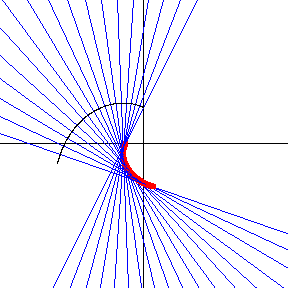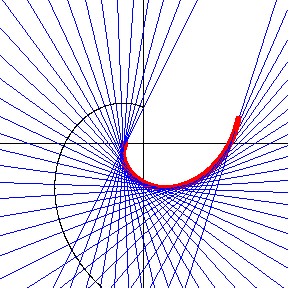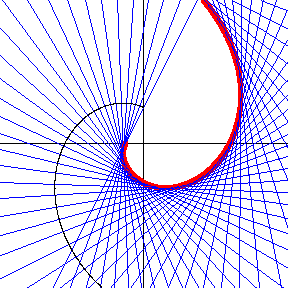
对于一个参数化表示为 对数螺线,
|
(1)
| |||
|
(2)
|
渐屈线 由下式给出
|
(3)
| |||
|
(4)
|
正如约翰·伯努利首次证明的那样,对数螺线 的 渐屈线 因此是另一个 对数螺线,具有 和
,
在某些情况下,渐屈线 与原曲线相同,这可以通过代换新变量来证明
|
(5)
|
然后上面的方程变为
|
(6)
| |||
|
(7)
| |||
|
(8)
| |||
|
(9)
|
如果满足以下条件,则这些方程等价于原始方程的形式
|
(10)
|
|
(11)
|
|
(12)
|
其中只有 中带有负号的解存在。求解得到下表总结的值。
| 1 | 0.2744106319... | |
| 2 | 0.1642700512... | |
| 3 | 0.1218322508... | |
| 4 | 0.0984064967... | |
| 5 | 0.0832810611... | |
| 6 | 0.0725974881... | |
| 7 | 0.0645958183... | |
| 8 | 0.0583494073... | |
| 9 | 0.0533203211... | |
| 10 | 0.0491732529... |