生命游戏是最著名的二维细胞自动机,由约翰·H·康威发明,并在马丁·加德纳于 1970 年 10 月开始的《科学美国人》专栏中普及。生命游戏最初是通过手工使用计数器进行(即,产生连续世代),但在计算机上的实现大大提高了探索模式的便利性。
生命细胞自动机的运行方式是在二维网格上放置一些填充的单元格。然后,每一代都会根据周围单元格的状态打开或关闭单元格。规则定义如下。检查当前单元格周围的所有八个单元格,看它们是否处于打开状态。任何处于打开状态的单元格都会被计数,然后使用此计数来确定当前单元格会发生什么。
1. 死亡:如果计数小于 2 或大于 3,则当前单元格关闭。
2. 生存:如果 (a) 计数正好为 2,或者 (b) 计数正好为 3 且当前单元格处于打开状态,则当前单元格保持不变。
3. 诞生:如果当前单元格处于关闭状态且计数正好为 3,则当前单元格打开。
生命游戏是一种全域细胞自动机,可以使用内置命令按如下方式实现CellularAutomaton,其中初始条件被指定为一个二进制矩阵 ,并返回世代
到
的结果。(这里,
对应于初始模式。)
Life[m_List?MatrixQ, {g1_Integer, g2_Integer}] :=
CellularAutomaton[
{
224,
{2, {{2, 2, 2}, {2, 1, 2}, {2, 2, 2}}},
{1, 1}
},
{m, 0},
g2,
{
{g1, g2},
Automatic
}] /; g2>=g1
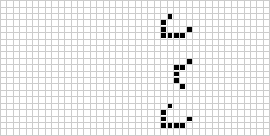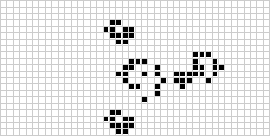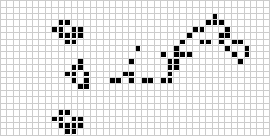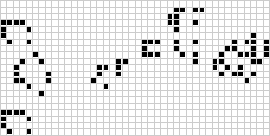
从一代到下一代不发生变化的模式被称为静止生命,并被称为具有周期 1。上面说明了几个静止生命。对于 个单元格,
, 2, 3, ... 的静止生命的数量为 0, 0, 0, 2, 1, 5, 4, 9, 10, 25, 46, 121, 240, 619, 1353, ... (OEIS A019473)。
在一组配置中循环的模式称为振荡器。
康威最初认为,没有任何模式可以产生无限数量的单元格,并向任何能在 1970 年底之前找到反例的人提供了 50 美元的奖金(Gardner 1983,第 216 页)。随后发现了许多反例,包括枪和喷射列车(如上图所示)。
没有父模式的生命模式被称为伊甸园(原因显而易见)。第一个这样的模式直到 1971 年才被发现,现在已知许多(LifeWiki)。

长期悬而未决的“唯一父问题”,即确定是否存在一种模式,该模式具有父模式但没有祖父模式(Wainwright 1972,Gardner 1983,第 249 页),由 Ilkka Törmä 和 Ville Salo 于 2022 年 1 月解决,他们发现了一个 374 个单元格的此类模式示例,这一结果很快被简化为上面说明的 306 个单元格的模式(apgoucher 2022,LifeWiki)。
令人惊讶的是,生命是一种通用细胞自动机,从某种意义上说,它实际上能够模拟任何细胞自动机、图灵机或任何其他可以转换为已知为通用的系统的系统。Berlekamp 等人 (1982) 和 Gosper (Gardner 1983, pp. 250-253) 独立给出了生命通用性的证明概要。2000 年左右,P. Rendell (Rendell, Adamatzky 2001) 在生命中显式实现了一个可以扩展为通用图灵机的图灵机。虽然 Rendell 的机器可以通过简单地将其磁带无限化而制成“真正的”通用计算机,但他既没有注意到这一事实,也没有提供通用图灵机的实际构造。随后,在 2002 年 11 月 11 日,P. Chapman 基于 D. Hickerson 的“滑动块内存”方法构建了一种生命模式,该模式实现了通用寄存器机的操作。与 Rendell 图灵机的有限磁带不同,Chapman 机器的寄存器中的值是无界的,这使其成为生命游戏中通用计算的真实模型。Chapman 的构造在 的区域中使用
个活动单元格,并且在 400 MHz 计算机上每秒可以计算大约 20 代。
更令人惊讶的是,正如 Wolfram (2002) 所表明的那样,即使是一维细胞自动机(特别是规则 110)也可以是通用的。
已经构建了类似于生命但具有不同规则的二维细胞自动机游戏,并命名为 HexLife 和 HighLife。HashLife 是一种生命算法,它通过将子模式存储在哈希表中并使用它们向前跳过,有时一次跳过数千代,从而实现显着的速度。