主题
Search

Bootstrap 渗流

DOWNLOAD Mathematica Notebook下载 Wolfram 笔记本

一个二维二元 (k=2) 全域细胞自动机，具有范围为 r=1 的 冯·诺依曼邻域。它具有一个出生规则，即其 4 个邻居中至少有 2 个是活着的，以及一个生存规则，即所有细胞都存活。n 步 Bootstrap 渗流在一个 s×s 网格上进行，初始条件为密度 p 的随机初始条件，可以在 Wolfram 语言中实现为

With[{n = 10, p = 0.1, s = 20},
  CellularAutomaton[
    {1018, {2, {{0, 2, 0}, {2, 1, 2}, {0, 2, 0}}},
      {1, 1}},
    Table[If[Random[Real] < p, 1, 0],  {s},  {s}],
    n
  ]
]
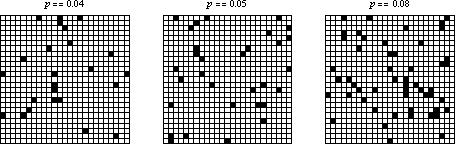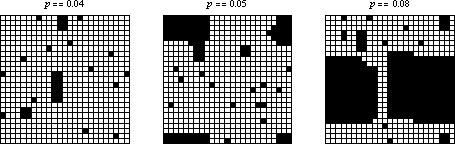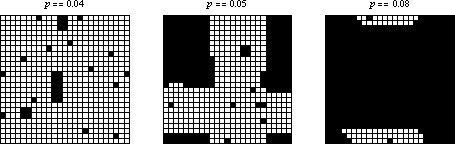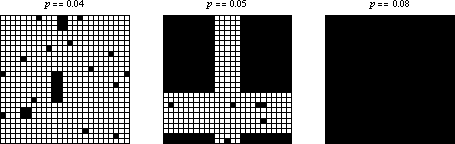
Bootstrap percolation for three different starting densities

如果初始条件由密度为 p 的细胞的随机稀疏排列组成，那么系统似乎会快速收敛到由活细胞的矩形岛屿和死细胞海洋包围的稳态。然而，当 p 跨越有限尺寸网格上的某个阈值时，行为似乎会发生变化，以至于每个细胞都变为活细胞。上面在三个 25×25 网格上显示了几个示例，这些网格具有随机初始条件和不同的起始密度。

然而，这个结论被证明是不正确的，因为行为的明显变化实际上是由于使用有限尺寸网格而引入的虚假边缘效应。令人惊讶的是，Holroyd (2003) 表明渐近阈值发生，使得

lim_(p->0; s->infty)plns=1/(18)pi^2.

另请参阅

全域细胞自动机, 投票模型

使用 探索

参考文献

Aizenman, M. and Lebowitz, J. "Metastability Effects in Bootstrap Percolation." J. Phys. A 21, 3801-3813, 1988.Gray, L. "A Mathematician Looks at Wolfram's New Kind of Science." Not. Amer. Math. Soc. 50, 200-211, 2003.Holroyd, A. "Sharp Metastability Threshold for Two-Dimensional Bootstrap Percolation." Prob. Th. and Related Fields 125, 195-224, 2003.Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, pp. 337-342, 2002.

在 上被引用

Bootstrap 渗流

请引用为

Weisstein, Eric W. "Bootstrap Percolation." 来自 —— 资源。 https://mathworld.net.cn/BootstrapPercolation.html

主题分类