蜘蛛和苍蝇问题考虑一个尺寸为 的长方体房间,蜘蛛位于其中一面
墙壁的中间,距离天花板一英尺。苍蝇位于对面墙壁的中间,距离地板一英尺。如果苍蝇保持静止,蜘蛛为了抓住苍蝇,沿着墙壁、天花板和地板爬行的最短总距离(即测地线)是多少?
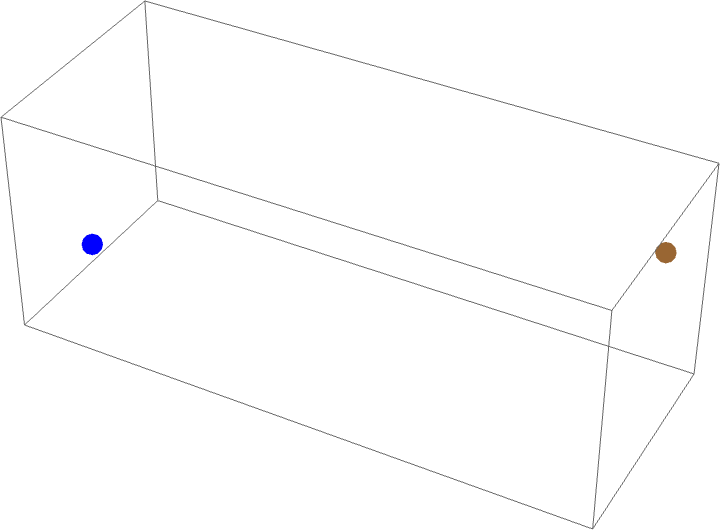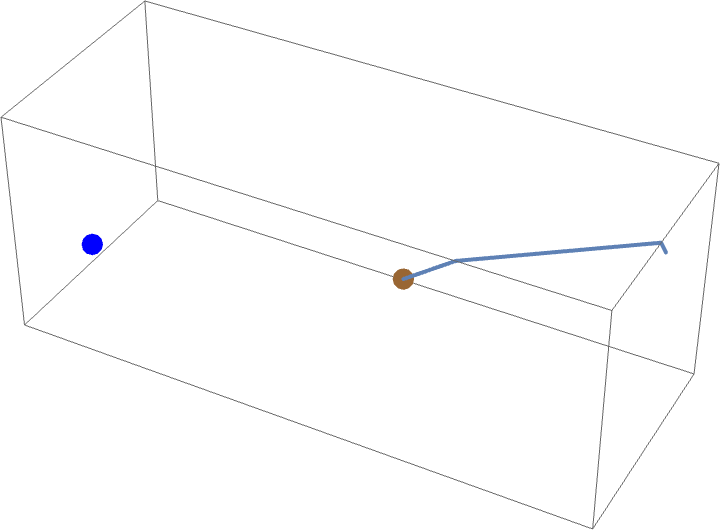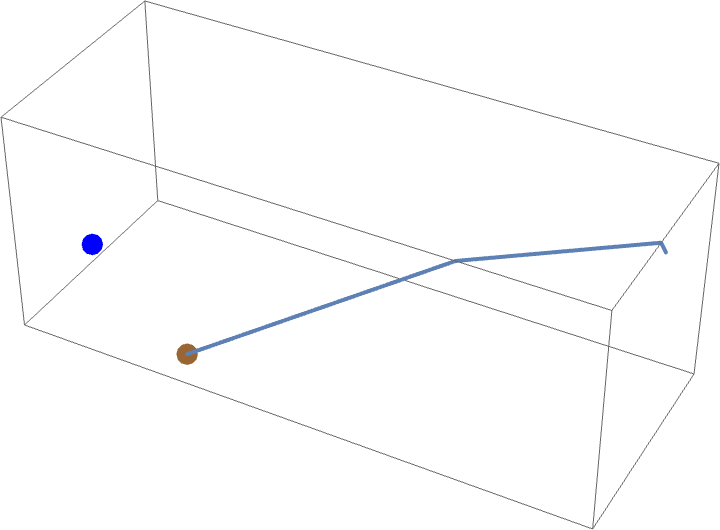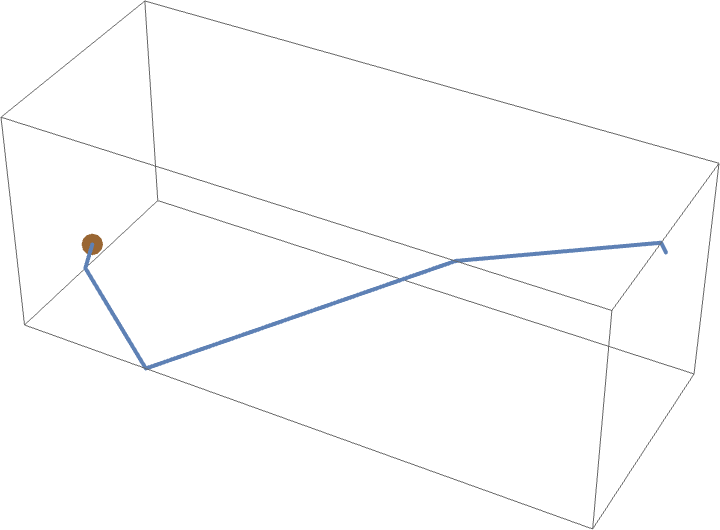
答案 可以通过如上所示的“展开”墙壁获得。请注意,这个距离比蜘蛛必须先沿着墙壁爬到地板,然后穿过地板,再向上爬一英尺才能到达苍蝇的
短。这个谜题最初由杜德尼于 1903 年在英国一家报纸上提出(Gardner 1958)。
这个问题的一个变体是,蜘蛛可以用蛛丝把自己悬挂起来,从而抄近路,而不必被迫粘在房间的表面上。如果蜘蛛在他的起始位置将一根蛛丝附着在墙上,然后把自己放到地板上(因此不爬行一英寸),那么他就可以步行穿过房间的长度 (),再向上爬一英尺,从而在总共爬行
后到达他的猎物(虽然总距离当然是
)。
如果蜘蛛不擅长将蛛丝固定在垂直墙壁上,他仍然可以通过仅爬行 来抓住苍蝇。特别是,他可以爬到天花板 (
),然后横穿天花板的长度 (
),再降低
(无需爬行),从而抓住苍蝇。