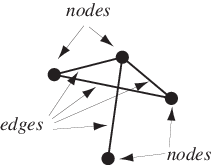
对于无向图,指定连接两个节点的线的无序节点对称为形成一条边。对于有向图,边是有序的节点对。“弧”、“分支”、“线”、“链接”和“1-单形”等术语有时用来代替边(例如,Skiena 1990,第 80 页;Harary 1994)。Harary (1994) 将图的边称为“线”。
下表列出了给定类别的所有图在 个节点上的边的总数。
| 图 | OEIS | |
| 图 | A086314 | 0, 1, 6, 33, 170, 1170, 10962, 172844, 4944024, ... |
| 标记图 | A095351 | 0, 1, 12, 192, 5120, 245760, 22020096, ... |
| 标记树 | A053506 | 0, 1, 6, 48, 500, 6480, ... |
| 种植树 | A055544 | 0, 1, 2, 6, 16, 45, 120, 336, 920, 2574, 7190, 20262, ... |
| 有根树 | A095350 | 0, 1, 4, 12, 36, 100, 288, 805, 2288, 6471, 18420, 52426, ... |
| 树 | A095349 | 0, 1, 2, 6, 12, 30, 66, 161, 376, 954, 2350, 6061, 15612, 41067, ... |