支配根

支配多项式的根称为支配根（Akbari 等人，2010年）。

给定图 的不同支配根的集合，其支配多项式为 ，可以表示为 （Akbari 等人，2010年）。Akbari 等人（2010年）表明，如果图 有两个不同的支配根，则 。此外，如果 是一个没有悬挂顶点的图且 ，则 的元素必须是 0、 或 （Akbari 等人，2010年）。如果允许悬挂顶点存在三个不同的支配根，则 也可能包括 。

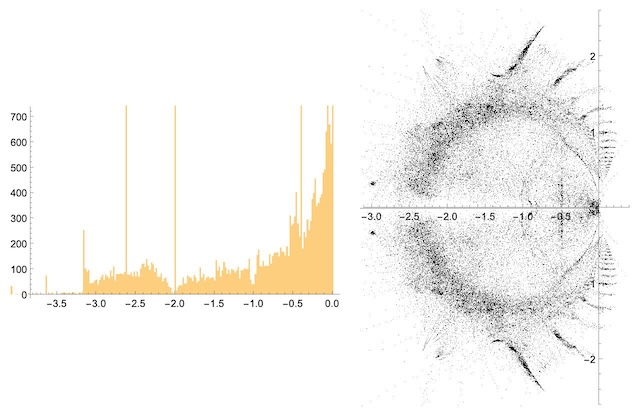
上面的图表显示了沿实轴的支配根的直方图，以及 GraphData 中图的支配根在复平面中的位置。GraphData.

最小的实支配根似乎出现在星形图中，对应于其支配多项式 的最小实根。

Akbari 等人（2010年）发现，顶点数为 6 或更少的图中没有包含 -1 的支配根，并推测这适用于所有图。这对于GraphData上面的直方图所示的 GraphData 中的所有图，以及顶点数最多为 10 的所有图（E. Weisstein，2024年11月26日）都是如此。此外，这些图的支配根中出现的唯一整数是 和 0（E. Weisstein，2024年12月1日）。