设 为
1, 2, ...,
的置换集合,并设
为
上的连续时间随机游走,它是以速率 1 执行随机选择的换位操作的结果。设
为在时间
从单位元
的距离,即返回到
所需的最少换位数。然后当
时,
,其中
 |
(Berestycki 2004;Berestycki 和 Durrett 2004),其中 被称为 Borel-Tanner 分布 (Trott 2006, p. 284)。
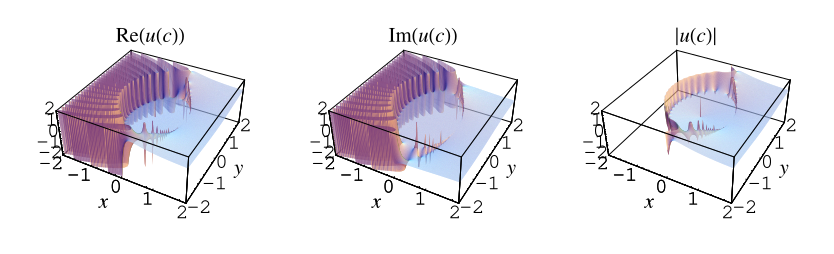
复数 的 Borel-Tanner 分布在复平面上方的图中绘制 (Trott 2006, p. 284)。
有趣的是,对于 ,此函数的值为
(Berestycki 2004;Trott 2006, p. 284)。